Big O

2022-04-06

Big O

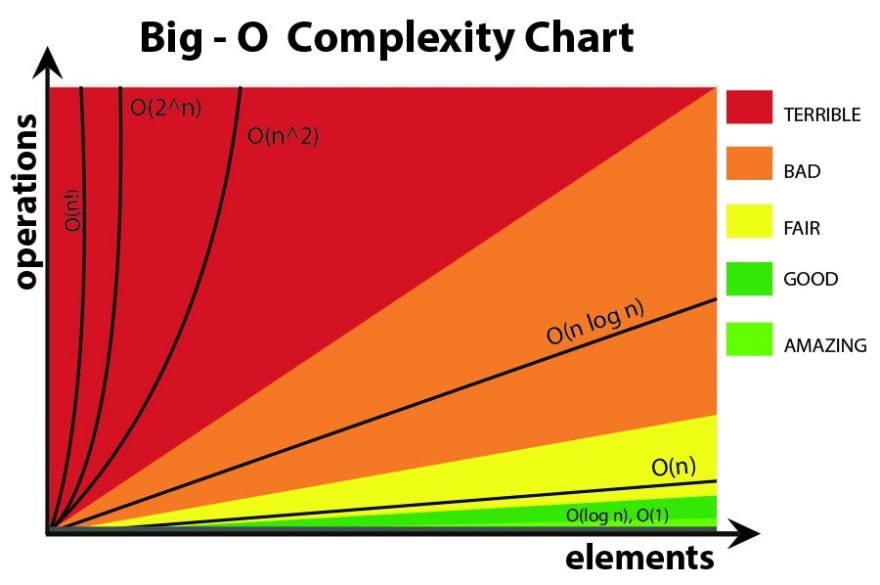
일반적으로 최악의 시나리오를 상정했을 때의 복잡도를 의미합니다. 알고리즘의 실제 러닝타임을 표시하기 보다는 데이터나 사용자의 증가율에 따른 알고리즘의 성능을 예측하는 게 목표입니다.
알고리즘의 성능을 수학적으로 표현해주는 표기법
알고리즘의 시간과 공간 복잡도를 표현할 수 있습니다.

O(1) Constant time

입력 데이터의 크기에 상관없이 언제나 일정한 시간이 걸리는 알고리즘입니다.

function timesTwo(num) {
	return 2 * num;
}
let result = timesTwo(5); // 10
let result2 = timesTwo(2000); // 4000

let arr = [1, 2, 3, 4];
// Adding and removing to the end of the array => Big (1) - constant time
arr.push(5); // [1, 2, 3, 4, 5]
arr.pop(); // [1, 2, 3]

어떤 숫자를 입력하든 계산하는 데는 같은 시간이 걸립니다. 이것을 constant time complexity 라고 합니다.

O(n) linear time

입력 데이터의 크기에 비례해서 처리 시간이 걸리는 알고리즘을 표현합니다.

const things = [ "a", "b", "c" ];
for (let i=0; i<things.length; i++>) {
	console.log(i);
}

하나의 for문을 계산해보겠습니다. things의 length인 3번 반복문이 동작하게 됩니다. things 배열의 길이가 늘어나게 된다면 늘어나는 만큼 반복문의 동작 횟수가 증가하게됩니다. 언제나 데이터와 시간이 같은 비율로 증가하기 때문에 그래프는 직선으로 표현됩니다.

function reverseArray(arr) {
	let newArr = [];
	for (let i = arr.length - 1; i >= 0; i--) {
		newArr.push(arr[i]);
	}
	return newArr;
}
const reversedArray1 = reverseArray([1, 2, 3]); // [3, 2, 1]
const reversedArray2 = reverseArray([1, 2, 3, 4, 5, 6]); // [6, 5, 4, 3, 2, 1]

reversedArray2의 연산 횟수가 reversedArray1보다 두 배 더 많습니다.

// Adding and removing to front of array => Big O(n) - linear time
arr.unshift(0); // [0, 1, 2, 3, 4]
arr.shift(); // [2, 3, 4]

O(n²) quadratic time

입력 데이터 크기의 제곱만큼 처리시간이 걸리는 알고리즘을 표현합니다.
배열의 길이가 늘어날 때마다 처리시간의 부담이 더 커집니다.

function multiplyAll(arr1, arr2) {
	if (arr1.length !== arr2.length) return undefined;
	let total = 0;
	for (let i of arr1) {
		for (let j of arr2) {
			total += i * j;
		}
	}
	return total;
}
let result1 = multiplyAll([1, 2], [5, 6]); // 33
let result2 = multiplyAll([1, 2, 3, 4], [5, 3, 1, 8]); // 170

총 작업 수는 첫 번째 배열의 길이와 두 번째 배열의 길이를 곱한 값이 됩니다.
위 예제는 Big O(3 * n²)를 갖습니다.
1. arr2의 모든 항목에 대한 loop (n²연산)
2. 두 숫자 곱하기 (또다른 n²연산)
3. total에 더하기 (또다른 n²연산)

O(nm) quadratic time

O(2^n) (n승) exponential time (2배씩 n번 늘어남)

입력이 1 증가할 때마다 연산 수가 2배씩 증가하는 알고리즘입니다.
이 알고리즘은 확장성이 매우 좋지 않으므로 피하는 것이 좋지만 O(2^n)가 가장 최악의 Big O는 아닙니다.

대표적인 것으로 피보나치수열이 있습니다.

function fibonacci(num) {
	// Base cases
	if (num === 0) {
		return 0;
	} else if (num === 1) {
		return 1;
	}
	// Recursive part
	return fibonacci(num - 1) + fibonacci(num - 2);
}
fibonacci(1); // 1
fibonacci(2); // 1
fibonacci(3); // 2
fibonacci(4); // 3
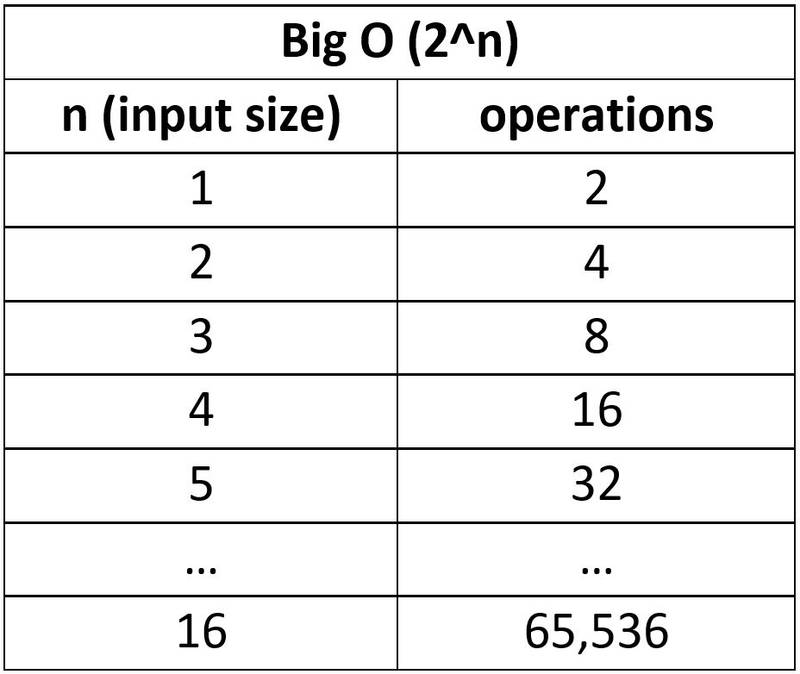
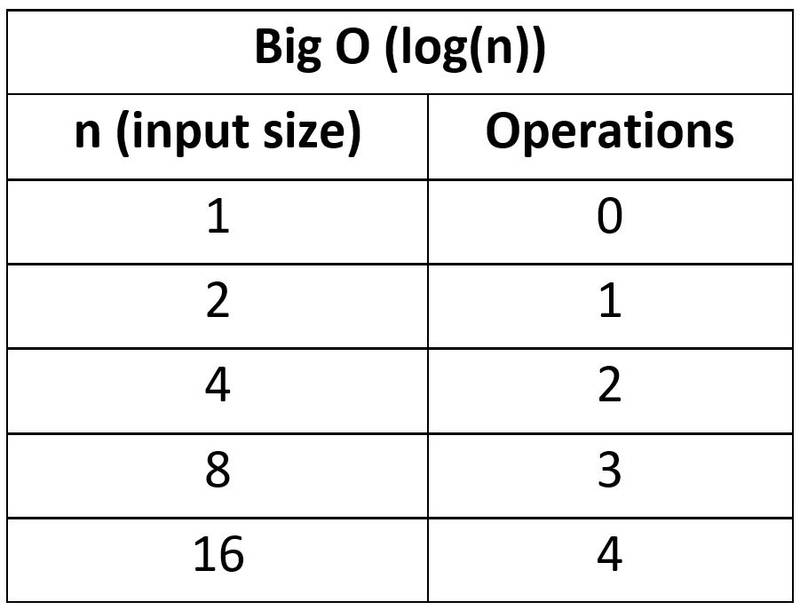
fibonacci(5); // 5

O(log n) Logarithmic Complexity

데이터가 커지면 커질수록 효율이 극대화됩니다.
검색 / 정렬 알고리즘의 꽃이며 보통 대규모 컬렉션을 처리할 때 가장 효율적인 방법
대표적인 것 : 이진탐색(binary search), 퀵정렬, 병합정렬

Log2(16) = x
2^x = 16
x = 4
: log는 다른 숫자를 얻기 위해 숫자(밑수)를 올려야 하는 거듭제곱입니다.
(수학에서 밑수가 지정되지 않은 경우(예: log(20))에는 일반적으로 10으로 가정됩니다. 그러나 컴퓨터 과학에서는 밑수가 지정되지 않은 경우 2로 가정합니다.

function logTime(arr) {
	let numberOfLoops = 0;
	for (let i = 1; i < arr.length; i *= 2) {
		numberOfLoops++;
	}
	return numberOfLoops;
}
let loopsA = logTime([1]); // 0 loops
let loopsB = logTime([1, 2]); // 1 loop
let loopsC = logTime([1, 2, 3, 4]); // 2 loops
let loopsD = logTime([1, 2, 3, 4, 5, 6, 7, 8]); // 3 loops
let loopsE = logTime(Array(16)); // 4 loops

for 루프에서 i의 현재 값을 2로 곱하므로 i는 1에서 2, 4, 8, 16…이 됩니다. 즉 루프마다 2배가 됩니다. 예제에서 볼 수 있듯이 입력 배열의 길이를 두 배로 늘릴 때마다 연산 수는 매회 1회씩 증가합니다. 연산의 수를 보면 입력의 크기가 계속 늘어나도 연산의 수는 그다지 늘어나지 않는 걸 볼 수 있습니다.

O(sqrt(n)) square root

O(n!) Factorial time complexity

최악의 알고리즘입니다.

function factorial(n) {
	let num = n;
	if (n === 0) return 1;
	for (let i = 0; i < n; i++) {
		num = n * factorial(n - 1);
	}
	return num;
}

factorial(1); // 0.02 ms
factorial(2); // 0.04 ms
factorial(10); // 42.08 ms
factorial(12); // 5231.54 ms => 5 seconds
factorial(13); // 69565.01 ms => 70 SECONDS!
factorial(14); // SMOKE & FLAMES!!

13만 입력해도 70초가 걸립니다.